
This means that the only force acting on it is the force of gravity.
PROJECTILE MOTION GRAPH FREE
Therefore, graph (C) correctly shows the changes in the kinetic energy of the objectīetween leaving the ground and returning to the ground.The equations that we are using to solve this problem only apply when the projectile is in free fall. Quadratically, reaches a minimum value, and then increases quadratically. This leaves us with graph (C), which has a nonzero initial kinetic energy, decreases

We know that this graph is incorrect because the kinetic energy is proportional to Time, reaches a minimum value, and then increases linearly with time. We see that graph (B) corresponds to a kinetic energy that decreases linearly over So the kinetic energy will increase proportional to the vertical velocity But since the kinetic energy is proportional to velocity squared, the kinetic energy But there is still some kinetic energy, because the horizontal velocity remainsįrom point 𝐵 to point 𝐶, the vertical velocity becomes negative and decreases at aĬonstant rate. At point 𝐵, the kinetic energy will be at its minimum, because the vertical velocity

The kinetic energy will decrease proportional to the vertical velocity squared. Velocity also decreases from point 𝐴 to point 𝐵. The kinetic energy must decrease from point 𝐴 to point 𝐵, because the vertical If we now consider the component of kinetic energy coming from the vertical velocity, This means we can immediately rule out graphs (A) and (D), since both show an initial Will always be a nonzero amount of kinetic energy throughout the projectile Since the horizontal velocity remains constant during the projectile motion, there So the kinetic energy will be proportional to the velocity squared.

The mass of the object does not change during the projectile motion. Squared, where 𝑚 is the mass and 𝑣 is the velocity. Now, we can recall that the equation for kinetic energy is given by half 𝑚𝑣 So this means that the horizontal component of the velocity will remain constant In addition, the acceleration of the object throughout its motion is entirely The object other than the force responsible for the initial horizontal velocity of The question does not indicate the presence of any force that acts horizontally on Now let’s consider the horizontal velocity. So we know how the vertical velocity of the object changes during the projectile And so the object falling back to the ground is in the downward direction, and the
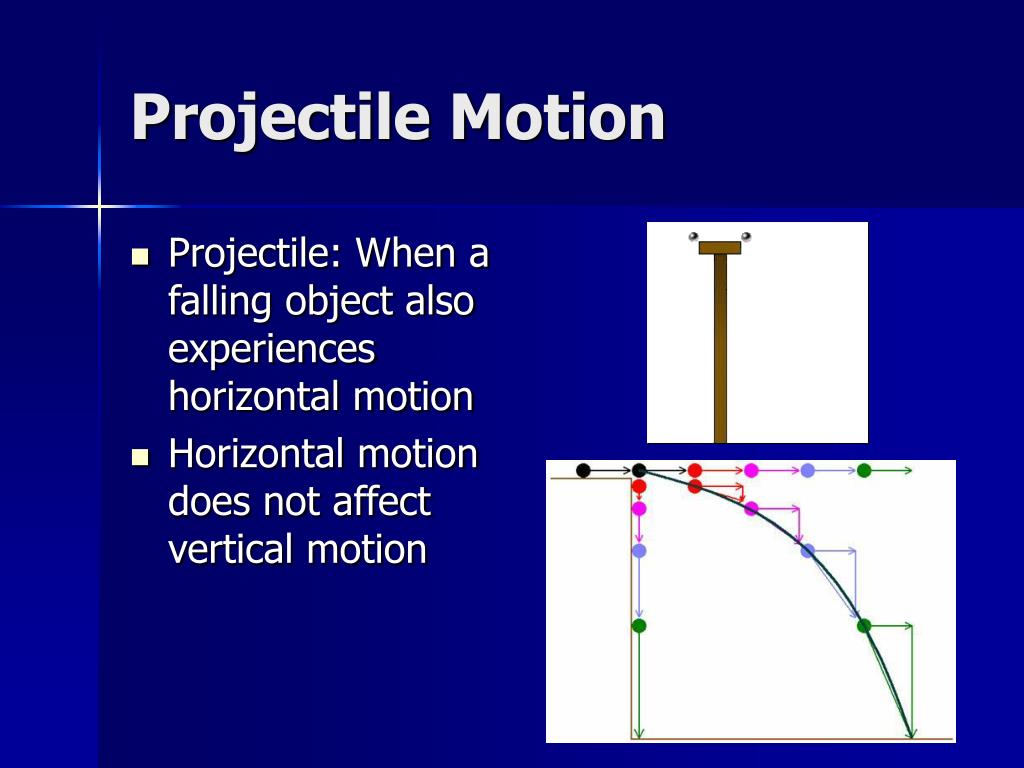
Here, we note that we’re taking the upward direction as positive. So the vertical velocity will decrease at the same constant rate as before. After point 𝐵, the object will begin to fall back down to the ground due to And at this point, the vertical velocity will be zero. Point 𝐵 is the highest point the object reaches. So the initial vertical velocity of the object will decrease at a constant rate until Uniform acceleration results in equal changes in speed in equal time intervals. So it accelerates downward uniformly throughout its entire motion due to the Let’s consider the vertical velocity for now. So this indicates that at point 𝐴, the object has an initial horizontal velocity andĪn initial vertical velocity, which are both nonzero. The kinetic energy of the object during projectile motion.įirst, we will look at the diagram. In this question, we want to determine the graph that correctly shows the changes in Leaving the ground and returning to the ground? (A), (B), (C), or (D). Which of these graphs shows the changes in the kinetic energy of the object between An object is set in motion by an initial force 𝐹 that acts diagonally upward, as


 0 kommentar(er)
0 kommentar(er)
